本章笔记有如下内容:
- 介绍向量化:接上文补充快速计算方法
- 向量化在逻辑回归中的应用
- 如何向量化逻辑回归
- Python的广播特性(Boardcasting)
- 在编写代码时容易遇到的错误,产生秩为1的非行非列向量组,以及避免方法
1.向量化
让代码运行的非常快的方法
在逻辑回归中,需要计算Z=wT*x +b(w和x都是列向量,w和x都输入nx维实数集),因此就需要两层遍历,来依次进行计算,就如同线性代数学科可以简化我们对方程求解一样,利用线性代数(Python中使用numpy库)来简化计算,利用引入特征值特征向量等等
PS:numpy是真的快,其本身是线性代数计算,在逻辑上优化了不少速度,而且还支持并行运算,效率真的很高。对于图像处理,对于一张图而言两层for和numpy是几秒钟和一瞬间的差别。
非向量化实现
z = 0
for i in range(n-x):
z += w[i] * x[i]
z += b
向量化实现
z = np.dot(w,x) + b 我在自己的电脑用jupyter跑了一下,对比了差别(for循环在1000000的级别下,运算速度慢了差不多300多倍)
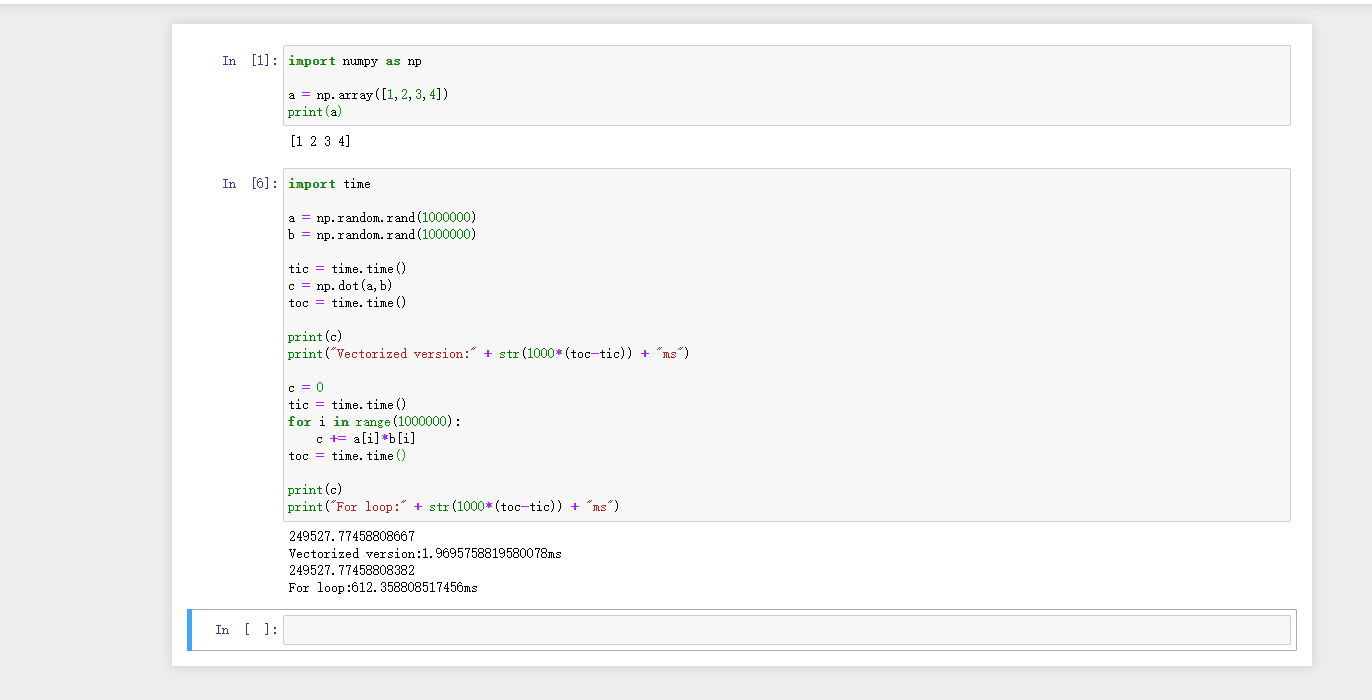
现在的深度学习训练,基本上实在GPU上面跑(因为GPU更加擅长并行),无论是GPU还是CPU,其都含有SIMD指令(单指令流多数据流,single instruction multiple data),Python的numpy利用了这样的指令进行并行计算,所以造成了这样的效果。
2.向量化在逻辑回归中的应用
对于整个逻辑回归而言,就可以用numpy的向量代替如下内容(绿色字迹)

3.向量化逻辑回归
注意复习一下线性代数,矩阵一章的内容

值得注意的地方是,整体来说 Z = w转置 * x + b,W是一个m维矩阵(表示有m个数据),而x有n个特征,但是b只是一个实数,直接使用如下代码就可以完成PPT中公式的相加
Z = np.dot(w.T , X) + bb作为一个实数(也可以理解为一个1*1维的矩阵),会自动的变成所求的1*m维的矩阵,这种设计思维在Python中称之为广播(Broadcasting),最终求出来的Z也是一个1*m维度的矩阵。(z ∈ Z ,Z1……Zm)
那么对于a而言又如何呢?a通过sigmoid函数对每一个z求得,实际上,可以直接把Z作为一个输入参数丢进sigmoid函数中,直接求出 A(a ∈ A, a1 …… am)。
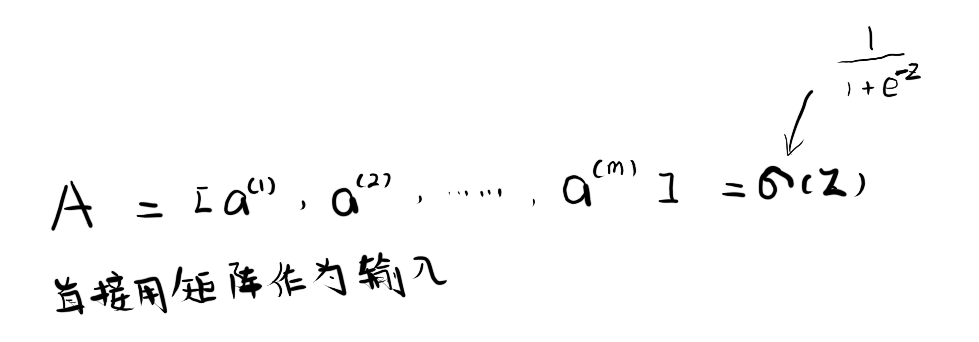
核心的核心就是:用矩阵代替for循环
接下来是梯度的输出

对于整个逻辑回归的核心代码而言,两个for循环都可以消去了,最后的效果为

(这里好像没有讲到成本函数J的推导)
4.Python的广播(Boardcasting)
给你一个食物表格数据,(每100克有)分别由 碳水化合物(Carbohydrates),蛋白质(proteins),以及脂肪(fats)三个特征组成,其中输入的食物种类有 苹果(Apples),牛肉(Beef),鸡蛋(Eggs),和土豆(Potatoes)组成
| apple | beef | eggs | potatoes | |
| carb | 56.0 | 0.0 | 4.4 | 68.0 |
| protein | 1.2 | 104.0 | 52.0 | 8.0 |
| fat | 1.8 | 135.0 | 99.0 | 0.9 |
PS:卡路里计算公式:碳水化合物 + 蛋白质 + 脂肪
对于苹果这一列,其中的卡路里含量是 56.0 + 1.2 + 1.8 = 59 卡路里,其中,来自碳水化合物的卡路里有 56/59 = 94.9% ……
对于卡路里而言,我们需要求解每一个食物种类的卡路里,问题是,可以不使用显示循环(for-loop)来进行此项操作么?
import numpy as np
A = np.array([
[56.0 , 0.0 , 4.4 , 68.0],
[1.2 , 104.0 , 52.0 , 8.0],
[1.8 , 135.0 , 99.0 , 0.9]
])
print(A)#output
[[ 56. 0. 4.4 68. ] [ 1.2 104. 52. 8. ] [ 1.8 135. 99. 0.9]]PS:在numpy中array,进行数据输出时,会自动消去无意义的小数点0,所以会造成输出出现了56. , 0. 这种奇怪的情况,其实就是 点 后全为0而已
接下来进行逐列相加
#计算总数,总的卡路里
cal = A.sum(axis=0)
#注意:axis = 0 - 竖直相加 ,1 - 水平相加
print(cal)#output
[ 59. 239. 155.4 76.9]
之后就要利用广播特性,直接进行不同规模尺度的矩阵相互乘除
#计算每一种成分在总的卡路里中占比多少
percentage = 100 * A/cal.reshape(1,4)
#注意此时cal已经是【1*4】矩阵了,使用reshape只是确保范围而已,可以去掉,不过建议都规范使用,其复杂度为O(1)
#利用了广播特性,A(3*4矩阵)/ cal(1*4矩阵)
print(percentage)#output
[[94.91525424 0. 2.83140283 88.42652796] [ 2.03389831 43.51464435 33.46203346 10.40312094] [ 3.05084746 56.48535565 63.70656371 1.17035111]]
广播(用一些图来解释,三种变换规则)

广播的核心规则:当一个(m*n)矩阵进行【+,-,*,/】对(1,n),(m,1),(1,1)四则运算时,都会自动使用复制的方式将其变成一个(m*n)矩阵,再进行运算得出结果;反过来,如果是一个(1,n),(m,1),(1,1)矩阵对一个(m*n)矩阵进行运算时,也会使用自动复制的方式制造为一个相等规模的(m,n)矩阵。
编写代码注意
有的时候Python因为他的便利性让很多的开发人员喜欢,当我们利用广播特性的时候,既不会报Type类型错误(行向量和列向量类型不一致)也不会报越界等错误,而是直接相加成功了,这种风格很方便编码,但是同时也会造成很多细微的,很难以让人琢磨的BUG。
比如,使用随机,生成5个高斯变量存储再数组a中
import numpy as np
a = np.random.randn(5)
print(a)output:
[-1.1915006 1.14112716 -0.3530684 1.63963826 0.50971633]
此时我们再输出一下a的shape
# 此时生成的 (5,) 既不是行向量,也不是列向量,就很奇怪
print(a.shape)output:
(5,)
可以发现,此时输出的(5,),所以这是所谓的Python秩为1的数组,但是,它既不是一个行向量,也不是一个列向量,所以当我们对a进行转置的时候(a.T)会发现和原来的数组还是一样的。
PS1:补充一下矩阵的转置(翻线性代数课本去):
矩阵转置:把行,换成同序数的列即可,一个特殊的概念a.T = a时说明a是一个对称矩阵 ,而当a.T = -a 的时候说明a为反对称矩阵
PS1:补充一下矩阵的秩,我推荐看这一篇知乎文章,可以快速理解https://www.zhihu.com/question/21605094 ,当然我更加推荐啃完整本线性代数的书,或者跟着一个考研老师系统学一遍
print(a.T)output:
[-1.1915006 1.14112716 -0.3530684 1.63963826 0.50971633]
a.T与a一样,此时我们再计算一下a和a.T的内积,你可能觉得a乘以a.T,或者说外积可能会得到一个矩阵,但是如果我们直接这样做的话,只会得到一个数字
print(np.dot(a,a.T))output:
5.79472651727104
所以建议在编写神经网络的时候,就不要使用这种数据结构,其中形状时(5,)或者(n,)这种秩为1的数组,相反如果你令a这种5*1矩阵的话,那么就可以得到令a变成5*1的列向量
a = np.random.randn(5,1)
print(a)output
[[-0.34963724] [-1.13975557] [-0.60878052] [ 0.02157292] [ 1.30132785]]
可以发现,在Python的numpy中,(5,1)和(5, )虽然看起来一样,而且这两个矩阵秩都是1,但是实际效果和作用缺大相径庭,(5,)仿佛不是一个矩阵,这样往往会造成很多不可以预估的BUG。
,当我们重新输出上面的求解,一切都变得正常了
print(a.T)output:
[[-0.34963724 -1.13975557 -0.60878052 0.02157292 1.30132785]]
以及使用np.dot求外积
#这样可以正确求得矩阵的外积
print(np.dot(a,a.T))output:
[[ 1.22246197e-01 3.98500987e-01 2.12852340e-01 -7.54269441e-03 -4.54992671e-01] [ 3.98500987e-01 1.29904276e+00 6.93860994e-01 -2.45878502e-02 -1.48319566e+00] [ 2.12852340e-01 6.93860994e-01 3.70613727e-01 -1.31331706e-02 -7.92223049e-01] [-7.54269441e-03 -2.45878502e-02 -1.31331706e-02 4.65390666e-04 2.80734352e-02] [-4.54992671e-01 -1.48319566e+00 -7.92223049e-01 2.80734352e-02 1.69345416e+00]]
PS:np.dot() 是一种比较灵活的求解方法,如果你的是一维矩阵,求解就是我们熟悉的内积,如果是二维矩阵,就是矩阵相乘

综上,我们可以得出结论,在实际编写代码中,应该养成一个习惯,就是对于自己创造的数据结构,需要对其进行验证,使用诸如 assert(a.shape == (5,1)) 这样的代码方法来确认是否数据结构满足预期,或者即时的使用 a = a.reshape( (5,1) )来调整自己的数据结构,以避免出现秩为一的非行非列矩阵造成奇怪的Bug。
0 条评论