说明:本文章为自己的笔记,以自己看的懂为标准,会省略一些内容
视频是在B站上面看的,连接为:https://www.bilibili.com/video/BV1FT4y1E74V
本章笔记记有如下内容:
- 结构化,非结构化数据
- Logistic回归基本概念
- sigmoid函数
- 损失函数
- 陈本函数
- 梯度下降方法
- 导数
- 计算图
- Logistic回归中梯度下降方法
- m个样本中Logistic回归的梯度下降
- 关于逻辑回归损失函数的解释
1.结构化数据(Structured Data),非结构化数据(Unstructured Data)
- 结构化数据:如数据库,每一个数据都有其对应的规范,比如 学生类里面有 学号,姓名,成绩等等,这些都属于结构化的数据
- 非结构化数据:如原始音频,图像,一段文字
结构化数据往往是计算机使用较为理想的,而非结构化数据往往指的是一些没有经过处理的,较为原始的数据。
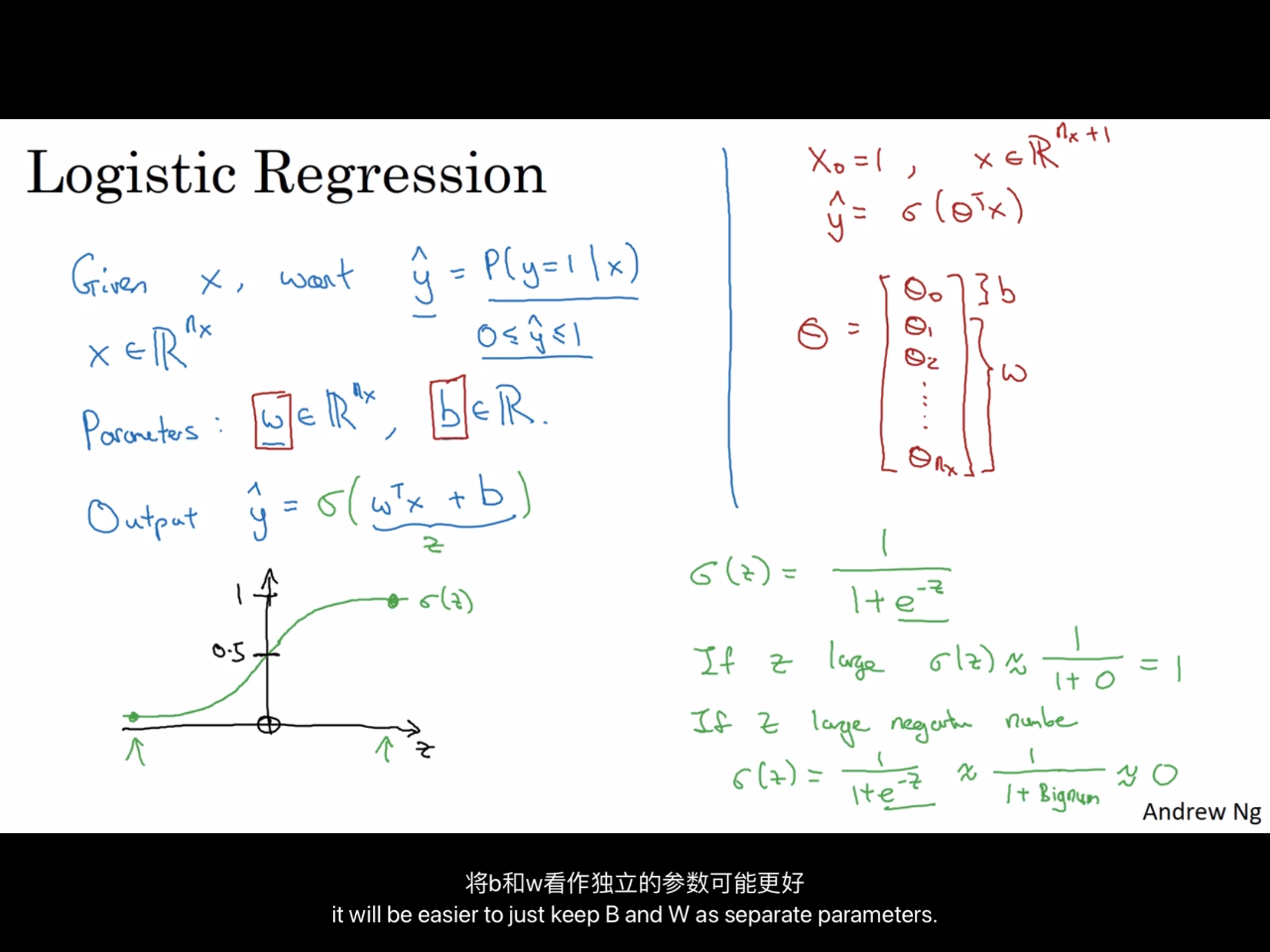
一.Logistic 逻辑回归
Logistic用于二分类(binary classification)算法
x输入 ——–> y输出

输入一张64*64彩色图片(假设是jpg,三通道,红绿蓝),特征向量x就是64*64*3 = 12288,分别就是三个通道的全部像素值,可以直接设 n = nx =12288,来表示输入的特征向量x的维度。
(x,y) 表示一个单独的样本 , y属于 {0,1}(二分样本)
我们常常用 m = m_train 表示训练样本 , m = m_test 表示测试样
X(大写),表示整个输入的矩阵,同理Y
Python中常用X.shape = (nx,m)这样取数据 ,Y.shape = (1,m)

1.:sigmoid函数
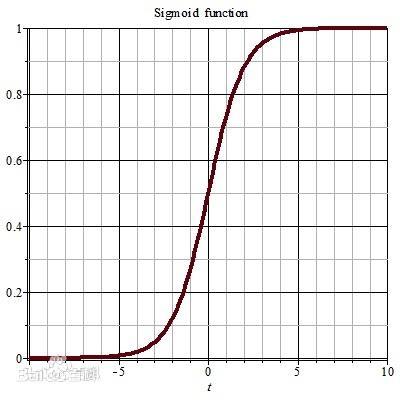
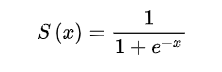

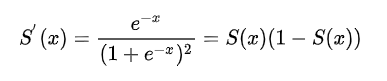

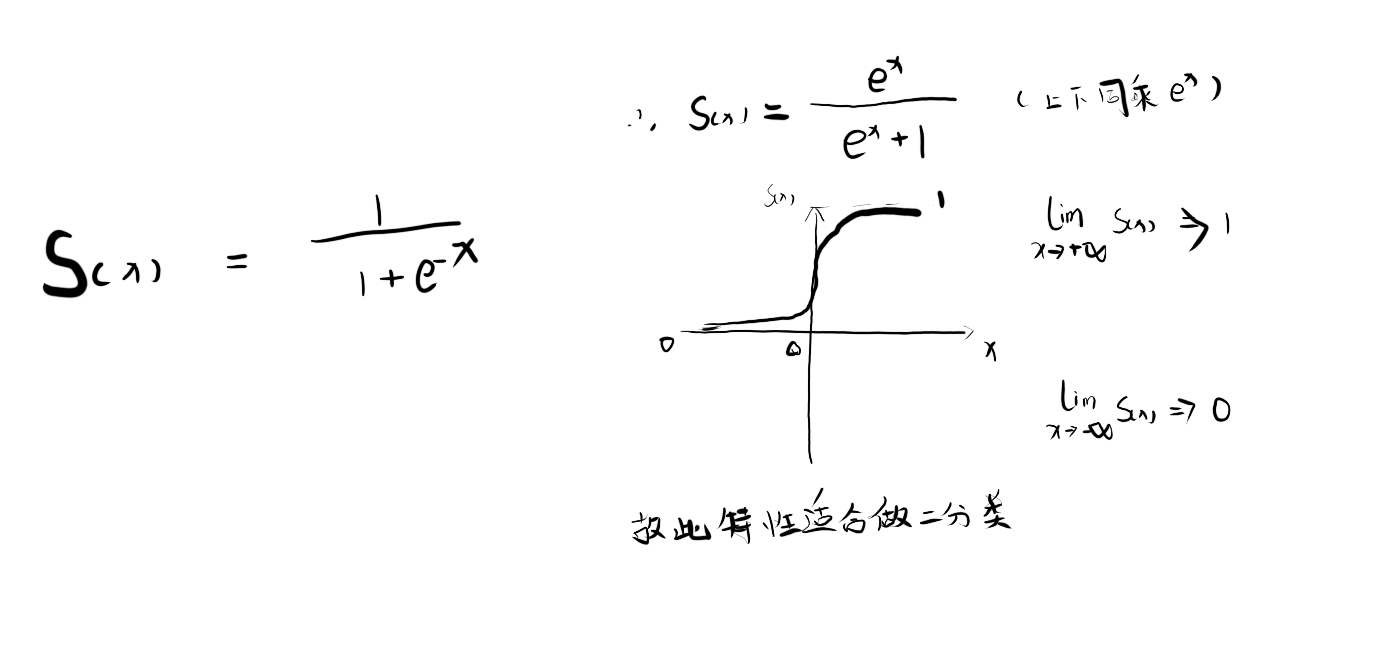
2.损失函数L
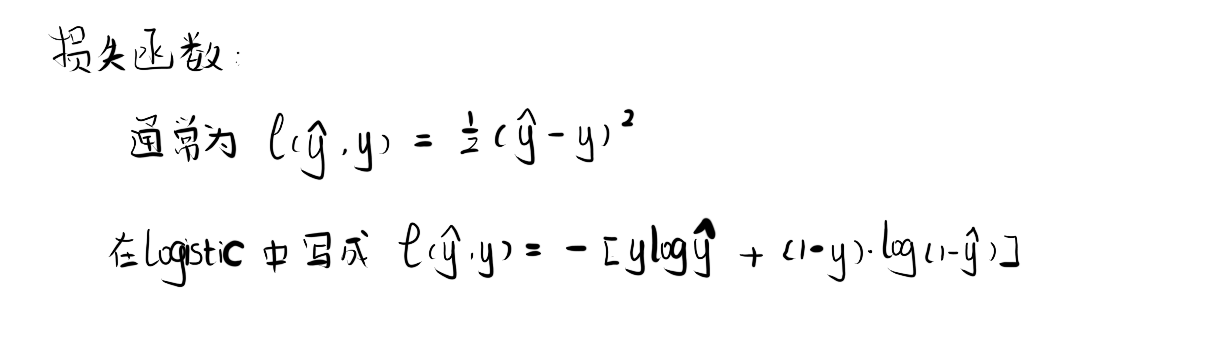
3.成本函数J
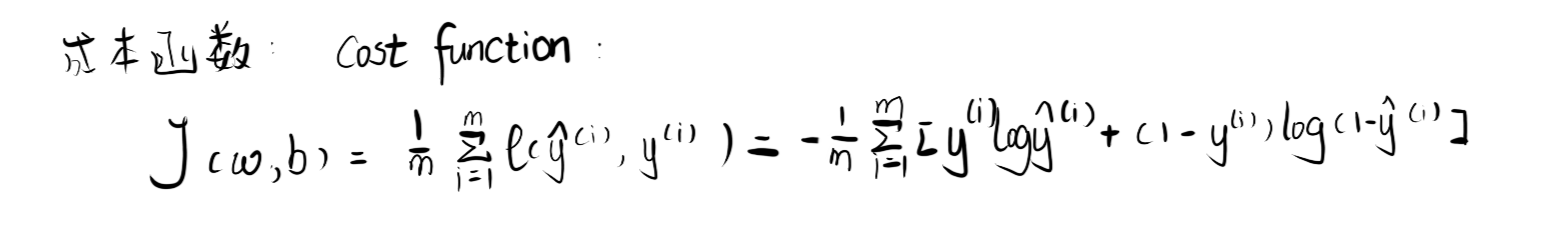
我们的目标就是要最小化风险函数,使得我们的拟合函数能够最大程度的对目标函数y进行拟合,
损失函数:衡量单一训练样例的效果成本函数:衡量参数w和b的效果在全部数据集上的效果
4.梯度下降方法

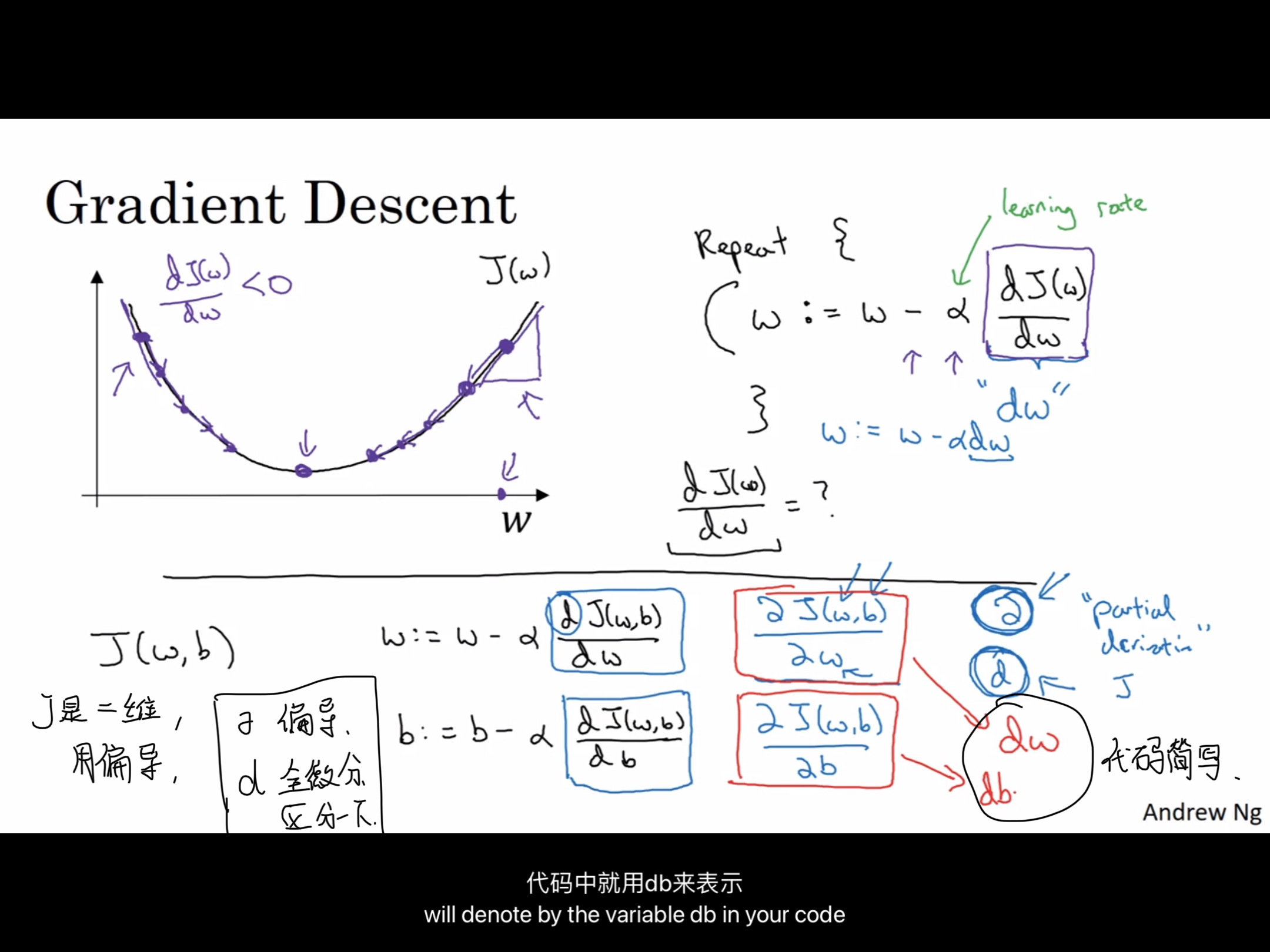
5.导数,
微积分:calculus导数:derivatives
6.计算图


7.逻辑回归中的梯度下降方法(单个)
参考本图,有两个输入,x1w1,x2w2,主要内容上面都可以找到,这个图解释了如何用来训练一个单个样本。但是实际情况是用数据集,有m个数据样本。

8.m个样本中的逻辑回归中的梯度下降
请先回顾一下成本函数J

计算中有两个缺点
- 两个for循环,1个是遍历m样本,2是遍历n特征,但是在深度学习中,在代码中显式使用for循环,会使得代码算法很低效,因为数据集会非常大,不用显式for循环,或者少用,将会很大程度上的帮助处理更大的数据,可以考虑使用一中向量化数据的方法(vectorization)帮助代码减少显式for循环。
9.关于逻辑回归损失函数的解释
回顾一下这个函数

然后将这两个if条件合并,就可以得到 p(y|x),成本函数,为什么最后添加负号,因为我们在逻辑回归中,需要最小化损失函数,因此最小化损失函数就是最大化log( p(y|x) )。

那么对于cost function成本函数呢?
假设所有的训练样本服从同一分布且相互独立,也就是 独立同分布的 ,所有这些样本的联合概率,就是每个样本概率的乘积,从1到m的p(y^(i) | x^(i))的概率乘积,要做最大似然估计,需要寻找一组参数,使得给定样本的观测值概率最大,但令这个概率最大化,等价于令其对数最大化。
所以对 Πp(y^(i) | x^(i)) 就会变成 ∑log p(y^(i) | x^(i) ),也等于 -L(y帽^(i) , y(i)),在统计学中,有一个方法,叫做最大似然估计(Maximun likelihood estimation)即:求出一组参数,使这个式子取最大值。
这样就可以推导出前面给出的logistic回归的,成本函数J(w,b),由于训练模型时,目标是让成本函数最小化,所以我们不是直接用最大似然估计概率,而是要去掉负号,最后为了方便,直接对成本函数进行进行一个1/m的缩放【注:某些老师的课程缩放可能是1/2m,这和实际情况有关】

对于似然的百科可以看这个:https://baike.baidu.com/item/%E6%9E%81%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1/3350286?fr=aladdin
0 条评论